1. Introduction
For more than one hundred years, the phenomenon of cardiac alternans has been recognized in the form of beat-to-beat alternated pulse magnitude (Traube,
1872). After the invention of the electrocardiography (ECG), T-wave alternans (periodic beat-to-beat variation in the amplitude or shape of the T-wave in an ECG) was observed and related with a poor prognosis (Windle,
1911). Due to the close association with the genesis of cardiac arrhythmias, clinically detected T-wave alternans has already proved useful for assessing the sudden cardiac death (SCD) risk (Rosenbaum et al.,
1994; Narayan,
2007). Shown in Fig.
1 is an example of cardiac alternans recorded in a normal Langendorff perfused guinea pig heart by Pruvot et al. (
2004). Alternations of T-wave in the ECG, action potential duration (APD), and Ca
2+ transient are illustrated from top to bottom. During the past decades, more and more researchers have focused on the phenomenon of cardiac alternans and have tried to identify the underlying mechanism. As shown in Fig.
1, experimental observations support the opinion that the phenomenon of cardiac alternans at the tissue level arises from the alternated repolarization at the cell level (Hoffman and Suckling,
1954; Kleinfeld et al.,
1963; Pruvot et al.,
2004). Cellular alternans has been observed in ventricular (Pruvot et al.,
2004; Cordeiro et al.,
2007; Gaeta et al.,
2009), atrial (Kockskamper and Blatter,
2002), and skeletal muscle cells (Zhao et al.,
2010). Up to now, two primary cellular mechanisms of alternans have been found from experiments and simulation studies. At a high pacing rate or under pathological conditions: (1) alternans can originate from the kinetics of the membrane voltage, which subsequently causes alternated intracellular Ca
2+ mainly through voltage-related L-type Ca
2+ channel (LCC) current (
I
CaL); (2) the instability of Ca
2+ handling dynamics leads to alternated intracellular Ca
2+, which then causes voltage alternans mainly by
I
CaL and Na
+-Ca
2+ exchange current (
I
NCX). However, due to the bi-directional coupling between membrane voltage kinetics and Ca
2+ handling dynamics, it is impossible to discern which is the primary or the secondary mechanism. Thus, a classic “unresolved chicken or egg problem” is raised, providing a big challenge to identify the origin of cardiac alternans.
Fig.1Alternated ECG, action potential (AP), and Ca
2+ transient by pacing at cycling length (CL) of 170 ms
Data are reproduced with permission from Pruvot et al. (
2004). These data were recorded simultaneously in the Langendorff perfused guinea pig heart during alternans
Heart failure (HF) is accompanied by the remodeling of ionic currents and Ca
2+ transport proteins. In addition to the usually observed prolonged APD, depressed Ca
2+ transient, and elevated Na
+ concentration, the heart rate threshold for the onset of APD alternans is observed to be significantly lowered in HF (Wilson et al.,
2009). Nevertheless, the governing factors underlying the enhanced susceptibility to alternans in HF are less understood. The possible effects of prolonged APD, decreased sarcoplasmic reticulum (SR) Ca
2+ pump (SERCA) function (O′Rourke et al.,
1999), increased SR Ca
2+ leak current (
I
leak) (Shannon et al.,
2003), and steeper fractional SR Ca
2+ release (Shannon et al.,
2005) on the behaviors of alternans in HF still need further research.
In this review, we focus on the progress of the research into the voltage- or Ca
2+-dependent cellular mechanism of alternans and show the role of theoretical analysis combined with experimental techniques in understanding the underlying mechanisms of alternans. The possible factors affecting the alternans behaviors in HF and which of them have the potential to be a therapeutic target are discussed. Finally, we also summarize the experimental and theoretical challenges, which may help us to better understand the mechanisms of alternans.
2. Cellular mechanism of cardiac alternans
2.1. APD restitution
APD restitution describes the relationship between APD and the previous diastolic interval (DI) (Fig.
2). Restitution has been attributed to the time-dependent repolarization or depolarization currents which govern the membrane voltage and APD. As cycling length (CL) decreases, accompanied with progressive shortening of DI, some ionic currents cannot completely recover from inactivation (depolarization currents) or some cannot inactivate (repolarization currents), resulting in progressively shorter APDs. Restitution was related with APD alternans (Nolasco and Dahlen,
1968). By treating the relationship between APD and DI analogous to an electronic amplifier with negative feedback, they used a simple graphical method (cobweb) to demonstrate that stable APD alternans occurs when the slope of the APD restitution curve is greater than or equal to one. Other groups also find similar results in both experiments and simulations (Karagueuzian et al.,
1993; Fox et al.,
2002). The restitution curve, a plot of APD against DI with the expression APD
n
+1=
f(DI
n
), is shown in Fig.
2b. DI
n
represents the interval between the end of the previous action potential and the next. When paced at a constant CL, the relationship DI
n
=CL−APD
n
is also plotted in Fig.
2b. According to the cobweb method (Nolasco and Dahlen,
1968), it is not difficult to show that when the slope is steep (≥1), a small perturbation would produce progressively growing APD oscillations until it reaches a steady-state alternans. In contrast, when the slope is flat (<1), a small perturbation would lead to casual damped oscillations and finally a stable 1:1 rhythm. It has been reported that a flattening APD restitution curve has an effect of depressing cardiac arrhythmias (Qu et al.,
2000; Fox et al.,
2002).
Fig.2
Standard APD restitution (a) and the relationship between its slope and the stability of APD alternans (b)
V
m represents the membrane voltage. Stable alternans can exist when slope≥1, and be absent when slope<1
Although this method provides an intuitive tool to analyze alternans, we have to point out that it is not universally valid. In some cases, alternans can be absent even when the restitution curve slope is >1 (Banville and Gray,
2002), and conversely alternans can still occur with the restitution curve slope <1 (Saitoh et al.,
1988). Basically, it does not incorporate the effect of alternans memory (Gilmour et al.,
1997) and ignores the impact of Ca
2+ handling dynamics (Pruvot et al.,
2004). The other refined restitution method, dynamic restitution (Koller et al.,
1998), cannot be expected to appreciate the cellular and sub-cellular processes controlling restitution either. Restitution could not reflect which currents are involved and to what degree each current affects alternans. During the last decade, more and more evidence has emerged and seemed to indicate that cellular alternans relies on the instability of the Ca
2+ handling dynamics.
2.2. Ca2+ handling dynamics
The ventricular intracellular Ca
2+ handling machinery is shown in Fig.
3a. Under control conditions, when depolarization begins, LCCs open and extracellular Ca
2+ crosses the sarcolemmal membrane to elevate the level of Ca
2+ in the subspace. Subsequently, Ca
2+ stored in SR is nearly synchronously triggered to release through ryanodine receptors (RyRs) in the form of thousands of individual Ca
2+ release units (CRUs), the release known as Ca
2+ sparks (Cheng et al.,
1993), and then cytosolic Ca
2+ is elevated after diffusion. During the abovementioned processes, SR acts as the main Ca
2+ storage organelle. To maintain the SR Ca
2+ content homeostasis, the amount of Ca
2+ released through RyRs must be balanced by the net Ca
2+ reloading into the SR by the SERCA pump current (
I
up) and
I
leak during each beat (i.e., ∫
I
RyRd
t=∫
I
upd
t−∫
I
leakd
t). Excitation-contraction (E-C) coupling gain, defined as the ratio of SR Ca
2+ release flux from RyRs to the flux of Ca
2+ entry by
I
CaL, is high to help the myocyte effectively contract under controlled conditions. However, in pathological conditions, the high E-C coupling gain can cause fluctuations in the Ca
2+ handling system. When the pacing rate is high or under pathological conditions, the cardiac myocyte fails to maintain SR Ca
2+ content homeostasis, resulting in SR Ca
2+ fluctuations and then alternated Ca
2+ transients from beat to beat. Because of the bi-directional coupling between membrane voltage kinetics and Ca
2+ handling dynamics, APD shows a secondary alternated phenomenon. Ca
2+→voltage coupling usually works in concordant (positive) mode (Saitoh et al.,
1988; Pruvot et al.,
2004), while discordant (negative) mode has already been found in ferret ventricular muscle (Kihara and Morgan,
1991) and rabbit papillary muscle (Wohlfart,
1982). As shown in Fig.
3b, concordant (discordant) Ca
2+→voltage coupling means that a larger Ca
2+ transient is accompanied with a longer (shorter) APD. On one hand, a larger Ca
2+ transient can enhance the inward current by increasing the driving force of
I
NCX to prolong the APD, but on the other hand, it can facilitate the inactivation of
I
CaL by Ca
2+-dependent inactivation to shorten the APD. Therefore, concordant (discordant) coupling corresponds to the case that increased
I
NCX (reduced
I
CaL) predominates over reduced
I
CaL (increased
I
NCX).
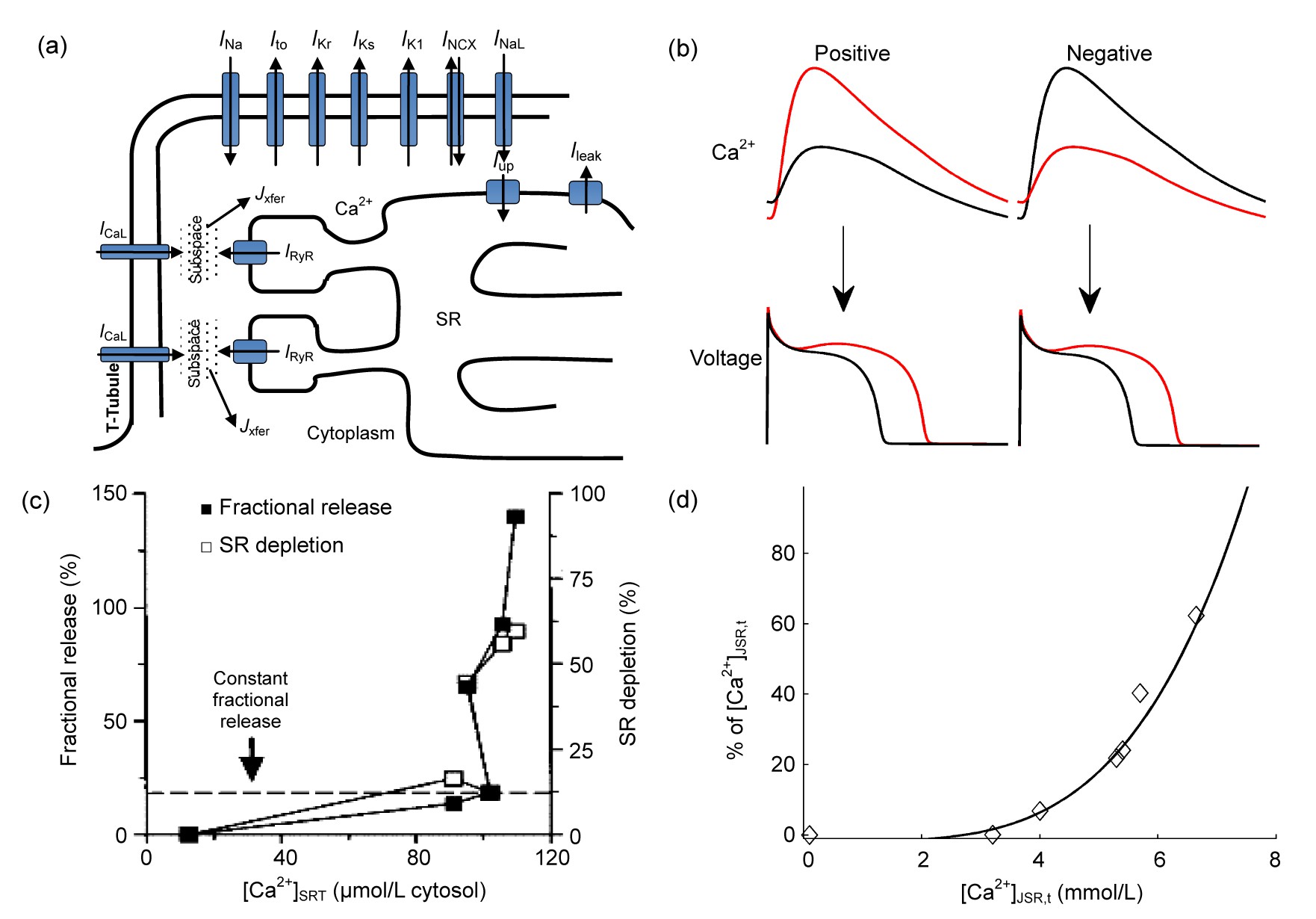
Fig.3Ca
2+ handling properties and Ca
2+-related alternans
(a) Schematic of the ventricular intracellular Ca
2+ handling components and the main ionic currents involved in depolarization and repolarization (
I
Na: fast Na
+ current;
I
to: transient outward K
+ current;
I
Kr: rapid delayed rectifier K
+ current;
I
Ks: slow delayed rectifier K
+ current;
I
K1: time-independent K
+ current;
I
NCX: Na
+-Ca
2+ exchange current;
I
NaL: late Na
+ current;
I
CaL: L-type Ca
2+ channel (LCC) current;
I
up: pump current;
I
leak: leak current;
I
RyR: ryanodine receptor current;
J
xfer: Ca
2+ flux transferred from subspace to the cytosol). (b) Illustration of positive and negative Ca
2+→voltage couplings. Positive (negative) coupling refers to the case that a larger Ca
2+ transient is accompanied with a longer (shorter) APD during the same beat at a constant CL. (c) Experimentally measured fractional SR Ca
2+ release as a function of [Ca
2+]
SRT (total Ca
2+ content in SR), reproduced with permission from Shannon et al. (
2000). (d) Simulated fractional SR Ca
2+ release from our work (Zang et al.,
2013). [Ca
2+]
JSR,t: total Ca
2+ content in junctional SR (JSR)
As to the mechanism of Ca
2+ handling instability, Diaz et al. (
2004) have related the instability to the steep relationship between SR Ca
2+ release and SR Ca
2+ content. In their experiment, the fractional SR Ca
2+ release is a smooth function of SR Ca
2+ content before the onset of alternans, but the function becomes much steeper as alternans occurs. In response to an increase in SR Ca
2+ content, the Ca
2+ release flux will accordingly increase, regulated by an SR controlling mechanism. If the feedback gain of this controlling mechanism is too high, a small alteration of SR Ca
2+ content will produce a large SR Ca
2+ release, resulting in a large alteration of SR Ca
2+ content and consequently fluctuations will occur (Diaz et al.,
2004; Eisner et al.,
2005). Figs.
3c and 3d are good examples of the steep fractional SR Ca
2+ release experimentally measured by Shannon et al. (
2000) and simulated by our new developed model (Zang et al.,
2013), respectively. As an important component of SR Ca
2+ cycling,
I
up is responsible for Ca
2+ reuptake into the SR and clearing the Ca
2+ in the cytoplasm. It has been found that decreased
I
up can promote Ca
2+ alternans (Wan et al.,
2005; Cordeiro et al.,
2007; Cutler et al.,
2009). Similarly, increased
I
leak can also play an important role in predisposing to alternans (Lehnart et al.,
2006). For the mechanisms mentioned above, the genesis of alternans is on the premise of SR Ca
2+ content fluctuation. On the contrary, SR Ca
2+ content remains the same before the large and small Ca
2+ transients (Huser et al.,
2000; Picht et al.,
2006), if the occurrence of alternans is due to the slow recovery from inactivation of RyRs (Dumitrescu et al.,
2002).
Following experimental findings, a large number of theoretical strategies have been developed and utilized to study the instability of Ca
2+ handling. Here, we just mention the most representative ones. Shiferaw et al. (
2003) have incorporated local Ca
2+ release dynamics into a model to explore the effect of both steep fractional SR Ca
2+ release and decreased
I
up on Ca
2+ alternans. Building upon the early experimental observations of their group (Diaz et al.,
1997;
2004), Tao et al. (
2008) have realized systolic alternans and supported the conclusion that steeper fractional SR Ca
2+ release is related with the threshold dependence of wave propagation. As the CLs decrease or under pathological conditions, not all RyRs are activated by the adjacent LCC. However, the fired Ca
2+ sparks by LCC can trigger the opening of adjacent RyRs and promote Ca
2+ wave propagation on the condition that the SR Ca
2+ content is above the threshold (Lu et al.,
2010). This wave causes the depletion of SR Ca
2+ content, indicating less SR Ca
2+ for the next beat. Consequently, for the next beat, a Ca
2+ wave rarely occurs and a small Ca
2+ transient is generated, because SR Ca
2+ content is below the threshold. Nevertheless, the occurrence of alternans in these models still relies on the SR Ca
2+ content fluctuations. Recently, Rovetti et al. (
2010) have developed a spatially distributed intracellular Ca
2+ handling model, in which Ca
2+ alternans could occur due to the RyR refractoriness without an SR Ca
2+ content fluctuation. In their model, Ca
2+ alternans occurs due to the three generic properties of the CRUs: randomness (Ca
2+ spark activation), refractoriness (CRU after a spark), and recruitment (Ca
2+ sparks inducing Ca
2+ sparks in adjacent CRUs).
The aforementioned experiment and simulation studies have demonstrated the special role of disturbed Ca
2+ handling in cardiac alternans. Furthermore, in the ventricular myocytes isolated from rabbits (Chudin et al.,
1999), guinea pigs (Wan et al.,
2005), and cats (Huser et al.,
2000), intracellular Ca
2+ transients can still alternate during voltage clamping. Some simulation studies (Shiferaw et al.,
2003; Livshitz and Rudy,
2007) not only reproduce the abovementioned experimental results, but find that AP alternans is absent when performing the Ca
2+ transient clamping. It seems that we are closer to the answer of the “chicken or egg problem” and the governing factor of alternans points to Ca
2+ handling instability. However, is this really the case? Indeed, these results could demonstrate that Ca
2+ handling instability is an inherent property of the cardiac myocytes, but it could not preclude the role of voltage kinetics in cellular alternans because Ca
2+ transient clamping may affect voltage kinetics and interfere with the possible predominant mechanism of alternans, finally leading to wrong conclusions. Jordan and Christini (
2007) have combined the techniques of AP voltage clamping, Ca
2+ transient clamping, and stability analysis to characterize the contribution of voltage- and Ca
2+-dependent coupling to AP stability. Fig.
4 shows the stability characteristics of the SSK model (Shiferaw et al.,
2005) with different parameter values:
u (the SR release slope) for
I
up and
τ
f (the time constant of voltage-dependent inactivation of the LCC) for Ca
2+-dependent inactivation time constant of
I
CaL, CVM model (Fox et al.,
2002), HRd model (Hund and Rudy,
2004), and TP model (ten Tusscher and Panfilov,
2006). In their analysis,
λ is a function of CL. |
λ|≤1 means that the 1:1 rhythm is stable and |
λ|>1 means that the 1:1 rhythm is unstable. Their results indicate that AP voltage clamping and Ca
2+ transient clamping do affect the predominant mechanism of cellular alternans. Both voltage- and Ca
2+-dependent mechanisms could be responsible for alternans, and sometimes the two factors may exist simultaneously as shown in the SSK model. The relative contribution of these two factors can also change according to corresponding physiological (pathological) conditions. This type of theoretical strategy combined with experimental techniques will be the key to solving the chicken or egg problem. Notice that Ca
2+ transient clamping is not feasible in experiments. However, by comparing the experimentally measured results of paced and AP-clamping protocol, we can still get valuable information about whether voltage or Ca
2+ is the predominant factor in regulating cellular alternans.
Fig.4Stability characteristics of the SSK model (a, b, c) (Shiferaw et al.,
2005) with different parameter values (
u and
τ
f), CVM model (d) (Fox et al.,
2002), HRd model (e) (Hund and Rudy,
2004), and TP model (f) (ten Tusscher and Panfilov,
2006)
λ is a function of cycling length (CL) for the above models during pacing (×), AP clamping (○), and Ca
2+ transient clamping (∆). |
λ|≤1 means that the 1:1 rhythm is stable and |
λ|>1 means that the 1:1 rhythm is unstable. Modified with permission from Figs. 4 and 6 of Jordan and Christini (
2007)
3. Heart failure and alternans
Previous studies have focused on alternans in normal rather than failing myocardium. In HF, some ionic currents and Ca
2+ transport proteins are remodeled, resulting in a longer APD, lowered Ca
2+ transient, elevated [Na
+], and enhanced propensity to the occurrence of alternans (O′Rourke et al.,
1999; Wilson et al.,
2009). According to the experimental reports (Wilson et al.,
2009), the CL needed to initiate alternans has increased from 240 to 500 ms for canine ventricular cells in HF. They attribute this increased propensity to the reduced expression of SERCA in HF. Moreover, the finding that Ca
2+ transients in ventricular cells prone to alternans (e.g., endocardial cells, corresponding to less distributed SERCA) have a longer decay time relative to those resistant to alternans (e.g., epicardial cells, corresponding to more distributed SERCA) also supports that idea (Cordeiro et al.,
2007). In addition to the reduced
I
up, alterations in
I
RyR and
I
leak may also be important factors affecting the occurrence of alternans (Xie et al.,
2008). Recently, we have developed a new theoretical model incorporating dynamic Ca/calmodulin-dependent protein kinase II (CaMKII) kinetics to explore the HF mechanisms (Zang et al.,
2013). As shown in Fig.
5a, APD in HF is prolonged due to the down-regulation of K
+ currents. Ca
2+ transient amplitude is lowered and diastolic Ca
2+ is elevated (Fig.
5c). Relative to the reduced
I
up, we identify the importance of enhanced
I
leak by over-expressed CaMKII in decreased Ca
2+ transient. The steep relationship between SR Ca
2+ release and SR Ca
2+ content is fitted by the following formula: fractional release=
a+
b([Ca
2+]
JSR,t)
n
, where [Ca
2+]
JSR,t represents the total Ca
2+ in the junctional SR (JSR), and
n represents the steepness. Under control condition, simulated alternans occurs at CL≤250 ms, with
n=4, while it occurs at CL≤530 ms with
n=5.4 in HF (Figs.
5b and 5d). The facilitation role of over-expressed CaMKII causes a steeper fractional SR Ca
2+ release in HF, which accounts for the enhanced susceptibility to alternans compared with control. Therefore, alternans could be eliminated with CaMKII inhibition in our analysis. Surprisingly, in our analysis, the effect of increased
I
up cannot depress alternans as some experiments have reported (Cutler et al.,
2009;
2012; Lyon et al.,
2011). First, it may be because we did not incorporate the influence of SERCA2a over-expression on CaMKII-regulated RyRs phosphorylation in our model. RyRs phosphorylation is reduced by SERCA2a gene therapy (Lyon et al.,
2011; Cutler et al.,
2012); Second, although increased
I
up has a direct elimination effect for alternans, it also indirectly increases SR Ca
2+ content, which predisposes to Ca
2+ content oscillations (Xie et al.,
2008). The effect of the
I
leak block is in the same case although some experiments find that the role of the
I
leak block in depressing alternans (Lehnart et al.,
2006). Until now, there are still no direct experimental data supporting our simulation results. However, we hope it will motivate further experimental characterization of Ca
2+ handling effects on alternans.
Fig.5Properties in heart failure (HF) compared with control
(a) Prolonged action potential (AP) in HF versus in control (
V
m: the membrane voltage); (b) The steep relationship in control and HF (
I
rel: SR release current; [Ca
2+]
JSR,t: total Ca
2+ content in junctional SR (JSR)); (c) Ca
2+ transient in control and HF ([Ca
2+]
i: intracellular Ca
2+); (d) Alternans threshold in control and HF against experimental data. Modified from Zang et al. (
2013)
Compared with Ca
2+ handling dynamics, it is easier to understand the effect of remodeled electrical factors involved in the propensity to alternans in HF. At a constant CL, APD is lengthened in HF compared with control, leading to a shorter DI for the depolarization (repolarization) currents to recover (inactivate), which facilitates the genesis of alternans at larger CLs. In HF, both voltage and Ca
2+-related components change, but it is still not able to identify their relative contribution to the easier alternans.
4. Clinical implications
Under pathological conditions such as myocardial ischemia (Qian et al.,
2003) or HF (Wilson et al.,
2009), alternans occurs at a much slower heart rate than that under controlled conditions. These conditions increase the propensity for cardiac arrhythmias like ventricular reentry and ventricular fibrillation (Walker and Rosenbaum,
2003). Relative to the spatially concordant alternans, the spatially discordant alternans is more arrhythmogenic, because it leads to the formation of the steepest gradients of refractory at the “nodal line” where out-of-phase regions are separated and alternans is absent (Konta et al.,
1990; Qu et al.,
2000). Spatially concordant alternans refers to the mode that all regions of the tissue alternate with the same phase, while spatially discordant alternans corresponds to the mode that some regions of the tissue alternate with the opposite phase to the other regions. The arrhythmogenesis caused by discordant alternans suggests why alternans is the precursor of cardiac arrhythmias and SCD in clinical situations (Walker and Rosenbaum,
2003). In HF, commonly observed fibrotic barriers and maldistribution of cardiac gap junctions have been found to lower the threshold for spatially discordant alternans (Pastore and Rosenbaum,
2000). In addition, as demonstrated in experiments (Wagner et al.,
2006) and in our simulation work (Zang et al.,
2013), fast Na
+ current in HF shows a delayed recovery from inactivation predisposing to spatially discordant alternans.
The existing interventions used to prevent VF by eliminating alternans usually have unexpected side effects because they do not target specific mechanisms and may not affect the predominant factors causing alternans. Riccio et al. (
1999) have used high-dose calcium channel blockers to depress alternans. On one hand, these channel blockers result in decreased Ca
2+ transient due to the lower SR Ca
2+ content caused by the less Ca
2+ influx, and on the other hand, conflicting results have been observed that the
I
CaL block promotes alternans (Li et al.,
2009). It is not difficult to understand the promotion effect. The
I
CaL block lowers the LCC open probability, resulting in the decreased amount of primary Ca
2+ sparks. Then the increased triggered secondary spark due to recruitment facilitates the formation of the Ca
2+ wave and promotes Ca
2+ alternans. Other potential therapeutic targets like SERCA2a gene therapy are promising (Cutler et al.,
2009;
2012; Lyon et al.,
2011). However, it is also found associated with a higher risk of acute mortality (Chen et al.,
2004). In addition, through theoretical analysis, we have found the inability of increasing SERCA to depress alternans. So, SERCA2a gene transfer still needs further testing and validation before the application can be used to cure patients with HF. Class-III antiarrhythmic agents, such as
d-sotalol, not only fail to depress arrhythmias but often provoke them, because these agents block K
+ currents and steepen APD restitution (Benson et al.,
2008) which may result in enhanced alternans.
The cellular mechanism of alternans in our new model (Zang et al.,
2013) may be due to the high fractional SR Ca
2+ release. Thus in our study, we have tested the role of CaMKII inhibition in the behaviors of alternans on the assumption that eliminating alternans at the cellular level also has the same antiarrhythmic effect at the tissue level. We found that by flattening the steep relationship between the SR Ca
2+ release and SR Ca
2+ content, CaMKII inhibition could effectively eliminate alternans without decreasing the Ca
2+ transient amplitude, indicating CaMKII may be a new therapeutic target. Some experimental observations also supported this result (Wu et al.,
2002; Kirchhof et al.,
2004).
As discussed above, it is of significant importance to develop experimental strategies to discern the causes of alternans and to quantify their relative contributions, so that more effective and targeted means of suppressing alternans and ventricular fibrillation can be found.
5. Future challenges
With the development of new experimental methods and theoretical techniques, a solution of the “chicken or egg problem” (i.e., the origin of alternans) may be possible.
Quantifying the properties of RyRs and CRUs under physiological conditions is technically challenging. Therefore, certain important features of Ca
2+-induced Ca
2+ release (CICR)-like RyR kinetics are limited and hard to reproduce, which constrain our understanding about the RyR refractory and Ca
2+ handling disability. In the future, high resolution optical imaging of the excitation-contraction coupling (ECC) domain ultrastructure and local Ca
2+ kinetics will help us better understand the Ca
2+ handling instability (Baddeley et al.,
2009; Greenstein and Winslow,
2011).
Although proposed theoretical strategies (Jordan and Christini,
2007; Sato et al.,
2007) may help us understand the driven factors of alternans, these strategies are still not able to differentiate the relative contribution of such factors. For example, if voltage kinetics plays the primary role, we still could not get the following information: which currents are involved? Does
I
CaL or
I
Kr play a role? What is the relative weight of each factor? It is highly important for us to develop one method so that we can identify the primary factor of alternans, which components of this mechanism are involved, and what is the relative weight of each other?
Existing clinical algorithms detecting T-wave alternans have proven useful and have been associated with the risk of SCD (Rosenbaum et al.,
1994; Narayan,
2007). However, it may sometimes fail to demonstrate a strong predictive value (Gold et al.,
2008). We predict that it may correspond to the situation of spatially concordant mode (Konta et al.,
1990; Qu et al.,
2000). In the future, developed techniques to identify spatially discordant alternans may improve the accuracy of arrhythmia risk assessments for the patients suffering from heart disease.
In conclusion, as new experimental techniques and theoretical strategies develop, more effective anti-arrhythmic therapeutic approaches are promising.
Acknowledgements
The authors would like to thank Dr. Rafael SHIMKUNAS from the University of California, Davis, USA for his help with editing this manuscript.
* Project supported by the National Basic Research Program (973) of China (No. 2007CB512100) and the National Natural Science Foundation of China (Nos. 81171421 and 61101046)Compliance with ethics guidelines Yun-liang ZANG and Ling XIA declare that they have no conflict of interest.References
[1] Baddeley, D., Jayasinghe, I.D., Lam, L., 2009. Optical single-channel resolution imaging of the ryanodine receptor distribution in rat cardiac myocytes.
PNAS, 106(52):22275-22280.


[2] Banville, I., Gray, R.A., 2002. Effect of action potential duration and conduction velocity restitution and their spatial dispersion on alternans and the stability of arrhythmias.
J Cardiovasc Electrophysiol, 13(11):1141-1149.


[3] Benson, A.P., Aslanidi, O.V., Zhang, H., 2008. The canine virtual ventricular wall: a platform for dissecting pharmacological effects on propagation and arrhythmogenesis.
Prog Biophys Mol Biol, 96(1-3):187-208.


[4] Chen, Y., Escoubet, B., Prunier, F., 2004. Constitutive cardiac overexpression of sarcoplasmic/endoplasmic reticulum Ca
2+-ATPase delays myocardial failure after myocardial infarction in rats at a cost of increased acute arrhythmias.
Circulation, 109(15):1898-1903.


[5] Cheng, H., Lederer, W.J., Cannell, M.B., 1993. Calcium sparks: elementary events underlying excitation-contraction coupling in heart muscle.
Science, 262(5134):740-744.


[6] Chudin, E., Goldhaber, J., Garfinkel, A., 1999. Intracellular Ca
2+ dynamics and the stability of ventricular tachycardia.
Biophys J, 77(6):2930-2941.


[7] Cordeiro, J.M., Malone, J.E., di Diego, J.M., 2007. Cellular and subcellular alternans in the canine left ventricle.
Am J Physiol Heart Circ Physiol, 293(6):H3506-H3516.


[8] Cutler, M.J., Wan, X., Laurita, K.R., 2009. Targeted SERCA2a gene expression identifies molecular mechanism and therapeutic target for arrhythmogenic cardiac alternans.
Circ Arrhythm Electrophysiol, 2(6):686-694.


[9] Cutler, M.J., Wan, X., Plummer, B.N., 2012. Targeted sarcoplasmic reticulum Ca
2+ ATPase 2a gene delivery to restore electrical stability in the failing heart.
Circulation, 126(17):2095-2104.


[10] Diaz, M.E., Trafford, A.W., ONeill, S.C., 1997. Measurement of sarcoplasmic reticulum Ca
2+ content and sarcolemmal Ca
2+ fluxes in isolated rat ventricular myocytes during spontaneous Ca
2+ release.
J Physiol, 501(1):3-16.


[11] Diaz, M.E., ONeill, S.C., Eisner, D.A., 2004. Sarcoplasmic reticulum calcium content fluctuation is the key to cardiac alternans.
Circ Res, 94(5):650-656.


[12] Dumitrescu, C., Narayan, P., Efimov, I.R., 2002. Mechanical alternans and restitution in failing SHHF rat left ventricles.
Am J Physiol Heart Circ Physiol, 282(4):H1320-H1326.


[13] Eisner, D.A., Diaz, M.E., Li, Y., 2005. Stability and instability of regulation of intracellular calcium.
Exp Physiol, 90(1):3-12.


[14] Fox, J.J., McHarg, J.L., Gilmour, R.F., 2002. Ionic mechanism of electrical alternans.
Am J Physiol Heart Circ Physiol, 282(2):H516-H530.


[15] Gaeta, S.A., Bub, G., Abbott, G.W., 2009. Dynamical mechanism for subcellular alternans in cardiac myocytes.
Circ Res, 105(4):335-342.


[16] Gilmour, R.F., Otani, N.F., Watanabe, M.A., 1997. Memory and complex dynamics in cardiac Purkinje fibers.
Am J Physiol, 272(4 Pt 2):H1826-H1832.

[17] Gold, M.R., Ip, J.H., Costantini, O., 2008. Role of microvolt T-wave alternans in assessment of arrhythmia vulnerability among patients with heart failure and systolic dysfunction: primary results from the T-wave alternans sudden cardiac death in heart failure trial substudy.
Circulation, 118(20):2022-2028.


[18] Greenstein, J.L., Winslow, R.L., 2011. Integrative systems models of cardiac excitation-contraction coupling.
Circ Res, 108(1):70-84.


[19] Hoffman, B.F., Suckling, E.E., 1954. Effect of heart rate on cardiac membrane potentials and the unipolar electrogram.
Am J Physiol, 179(1):123-130.

[20] Hund, T.J., Rudy, Y., 2004. Rate dependence and regulation of action potential and calcium transient in a canine cardiac ventricular cell model.
Circulation, 110(20):3168-3174.


[21] Huser, J., Wang, Y.G., Sheehan, K.A., 2000. Functional coupling between glycolysis and excitation-contraction coupling underlies alternans in cat heart cells.
J Physiol, 524(3):795-806.


[22] Jordan, P.N., Christini, D.J., 2007. Characterizing the contribution of voltage- and calcium-dependent coupling to action potential stability: implications for repolarization alternans.
Am J Physiol Heart Circ Physiol, 293(4):H2109-H2118.


[23] Karagueuzian, H.S., Khan, S.S., Hong, K., 1993. Action potential alternans and irregular dynamics in quinidine-intoxicated ventricular muscle cells. Implications for ventricular proarrhythmia.
Circulation, 87(5):1661-1672.


[24] Kihara, Y., Morgan, J.P., 1991. Abnormal Ca
i
2+ handling is the primary cause of mechanical alternans: study in ferret ventricular muscles.
Am J Physiol, 261(6 Pt 2):H1746-H1755.

[25] Kirchhof, P., Fabritz, L., Kilic, A., 2004. Ventricular arrhythmias, increased cardiac calmodulin kinase II expression, and altered repolarization kinetics in ANP receptor deficient mice.
J Mol Cell Cardiol, 36(5):691-700.


[26] Kleinfeld, M., Stein, E., Kossmann, C.E., 1963. Electrical alternans with emphasis on recent observations made by means of single-cell electrical recording.
Am Heart J, 65(4):495-500.


[27] Kockskamper, J., Blatter, L.A., 2002. Subcellular Ca
2+ alternans represents a novel mechanism for the generation of arrhythmogenic Ca
2+ waves in cat atrial myocytes.
J Physiol, 545(1):65-79.


[28] Koller, M.L., Riccio, M.L., Gilmour, R.F., 1998. Dynamic restitution of action potential duration during electrical alternans and ventricular fibrillation.
Am J Physiol, 275(5 Pt 2):H1635-H1642.

[29] Konta, T., Ikeda, K., Yamaki, M., 1990. Significance of discordant ST alternans in ventricular fibrillation.
Circulation, 82(6):2185-2189.


[30] Lehnart, S.E., Terrenoire, C., Reiken, S., 2006. Stabilization of cardiac ryanodine receptor prevents intracellular calcium leak and arrhythmias.
PNAS, 103(20):7906-7910.


[31] Li, Y., Diaz, M.E., Eisner, D.A., 2009. The effects of membrane potential, SR Ca
2+ content and RyR responsiveness on systolic Ca
2+ alternans in rat ventricular myocytes.
J Physiol, 587(6):1283-1292.


[32] Livshitz, L.M., Rudy, Y., 2007. Regulation of Ca
2+ and electrical alternans in cardiac myocytes: role of CAMKII and repolarizing currents.
Am J Physiol Heart Circ Physiol, 292(6):H2854-H2866.


[33] Lu, L., Xia, L., Ye, X., 2010. Simulation of the effect of rogue ryanodine receptors on a calcium wave in ventricular myocytes with heart failure.
Phys Biol, 7(2):026005


[34] Lyon, A.R., Bannister, M.L., Collins, T., 2011. SERCA2a gene transfer decreases sarcoplasmic reticulum calcium leak and reduces ventricular arrhythmias in a model of chronic heart failure.
Circ Arrhythm Electrophysiol, 4(3):362-372.


[35] Narayan, S.M., 2007. Is T-wave alternans as good or better than programmed ventricular stimulation?.
Heart Rhythm, 4(7):913-915.


[36] Nolasco, J.B., Dahlen, R.W., 1968. A graphic method for the study of alternation in cardiac action potentials.
J Appl Physiol, 25(2):191-196.

[37] ORourke, B., Kass, D.A., Tomaselli, G.F., 1999. Mechanisms of altered excitation-contraction coupling in canine tachycardia-induced heart failure, I: experimental studies.
Circ Res, 84(5):562-570.


[38] Pastore, J.M., Rosenbaum, D.S., 2000. Role of structural barriers in the mechanism of alternans-induced reentry.
Circ Res, 87(12):1157-1163.


[39] Picht, E., DeSantiago, J., Blatter, L.A., 2006. Cardiac alternans do not rely on diastolic sarcoplasmic reticulum calcium content fluctuations.
Circ Res, 99(7):740-748.


[40] Pruvot, E.J., Katra, R.P., Rosenbaum, D.S., 2004. Role of calcium cycling versus restitution in the mechanism of repolarization alternans.
Circ Res, 94(8):1083-1090.


[41] Qian, Y.W., Sung, R.J., Lin, S.F., 2003. Spatial heterogeneity of action potential alternans during global ischemia in the rabbit heart.
Am J Physiol Heart Circ Physiol, 285(6):H2722-H2733.


[42] Qu, Z., Garfinkel, A., Chen, P.S., 2000. Mechanisms of discordant alternans and induction of reentry in simulated cardiac tissue.
Circulation, 102(14):1664-1670.


[43] Riccio, M.L., Koller, M.L., Gilmour, R.F., 1999. Electrical restitution and spatiotemporal organization during ventricular fibrillation.
Circ Res, 84(8):955-963.


[44] Rosenbaum, D.S., Jackson, L.E., Smith, J.M., 1994. Electrical alternans and vulnerability to ventricular arrhythmias.
N Engl J Med, 330(4):235-241.


[45] Rovetti, R., Cui, X., Garfinkel, A., 2010. Spark-induced sparks as a mechanism of intracellular calcium alternans in cardiac myocytes.
Circ Res, 106(10):1582-1591.


[46] Saitoh, H., Bailey, J.C., Surawicz, B., 1988. Alternans of action potential duration after abrupt shortening of cycle length: differences between dog Purkinje and ventricular muscle fibers.
Circ Res, 62(5):1027-1040.


[47] Sato, D., Shiferaw, Y., Qu, Z., 2007. Inferring the cellular origin of voltage and calcium alternans from the spatial scales of phase reversal during discordant alternans.
Biophys J, 92(4):L33-L35.


[48] Shannon, T.R., Ginsburg, K.S., Bers, D.M., 2000. Potentiation of fractional sarcoplasmic reticulum calcium release by total and free intra-sarcoplasmic reticulum calcium concentration.
Biophys J, 78(1):334-343.


[49] Shannon, T.R., Pogwizd, S.M., Bers, D.M., 2003. Elevated sarcoplasmic reticulum Ca
2+ leak in intact ventricular myocytes from rabbits in heart failure.
Circ Res, 93(7):592-594.


[50] Shannon, T.R., Wang, F., Bers, D.M., 2005. Regulation of cardiac sarcoplasmic reticulum Ca release by luminal [Ca] and altered gating assessed with a mathematical model.
Biophys J, 89(6):4096-4110.


[51] Shiferaw, Y., Watanabe, M.A., Garfinkel, A., 2003. Model of intracellular calcium cycling in ventricular myocytes.
Biophys J, 85(6):3666-3686.


[52] Shiferaw, Y., Sato, D., Karma, A., 2005. Coupled dynamics of voltage and calcium in paced cardiac cells.
Phys Rev E, 71(2 Pt 1):021903

[53] Tao, T., O'Neill, S.C., Diaz, M.E., 2008. Alternans of cardiac calcium cycling in a cluster of ryanodine receptors: a simulation study.
Am J Physiol Heart Circ Physiol, 295(2):H598-H609.


[54] ten Tusscher, K.H., Panfilov, A.V., 2006. Alternans and spiral breakup in a human ventricular tissue model.
Am J Physiol Heart Circ Physiol, 291(3):H1088-H1100.


[55] Traube, L., 1872. Ein Fall von Pulsus bigeminus nebst Bemerkungen über die Leberschwellungen bei Klappenfehlern und über acute Leberatrophie.
Berlin Klin Wochenschr, (in German),9:185-188.
[56] Wagner, S., Dybkova, N., Rasenack, E.C., 2006. Ca
2+/calmodulin-dependent protein kinase II regulates cardiac Na
+ channels.
J Clin Invest, 116(12):3127-3138.


[57] Walker, M.L., Rosenbaum, D.S., 2003. Repolarization alternans: implications for the mechanism and prevention of sudden cardiac death.
Cardiovasc Res, 57(3):599-614.


[58] Wan, X., Laurita, K.R., Pruvot, E.J., 2005. Molecular correlates of repolarization alternans in cardiac myocytes.
J Mol Cell Cardiol, 39(3):419-428.


[59] Wilson, L.D., Jeyaraj, D., Wan, X., 2009. Heart failure enhances susceptibility to arrhythmogenic cardiac alternans.
Heart Rhythm, 6(2):251-259.


[60] Windle, J.D., 1911. The incidence and prognostic value of the pulsus alternans in myocardial and arterial disease.
Quart J Med, 6(2617):453-462.
[61] Wohlfart, B., 1982. Analysis of mechanical alternans in rabbit papillary muscle.
Acta Physiol Scand, 115(4):405-414.


[62] Wu, Y., Temple, J., Zhang, R., 2002. Calmodulin kinase II and arrhythmias in a mouse model of cardiac hypertrophy.
Circulation, 106(10):1288-1293.


[63] Xie, L.H., Sato, D., Garfinkel, A., 2008. Intracellular Ca alternans: coordinated regulation by sarcoplasmic reticulum release, uptake, and leak.
Biophys J, 95(6):3100-3110.


[64] Zang, Y., Dai, L., Zhan, H., 2013. Theoretical investigation of the mechanism of heart failure using a canine ventricular cell model: especially the role of up-regulated CaMKII and SR Ca
2+ leak.
J Mol Cell Cardiol, 56:34-43.


[65] Zhao, X., Yamazaki, D., Park, K.H., 2010. Ca
2+ overload and sarcoplasmic reticulum instability in
tric-a null skeletal muscle.
J Biol Chem, 285(48):37370-37376.




























































































































Open peer comments: Debate/Discuss/Question/Opinion
<1>